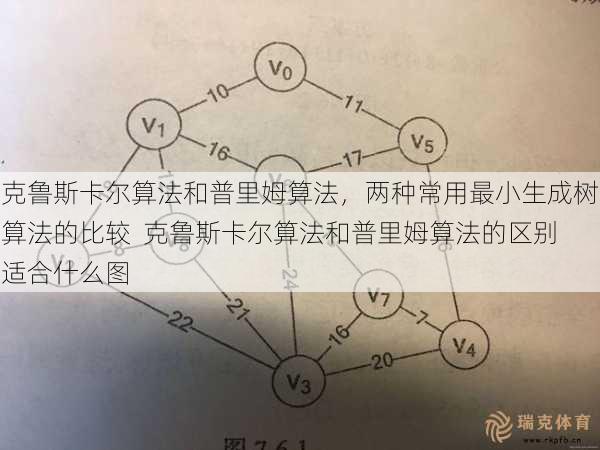
克鲁斯卡尔算法和普里姆算法，两种常用最小生成树算法的比较 克鲁斯卡尔算法和普里姆算法的区别适合什么图

本文主要涉及的问题是克鲁斯卡尔算法和普里姆算法，这两种算法都是常用的最小生成树算法。在本文中，我们将对这两种算法进行详细的比较和解释。

1. 什么是最小生成树算法？

最小生成树算法是在一个连通无向图中，找出一棵生成树，使得这棵生成树的所有边的权值之和最小。最小生成树算法可以用来解决许多实际问题，如 *** 设计、电路设计等。

2. 克鲁斯卡尔算法的原理是什么？

克鲁斯卡尔算法是一种贪心算法，它的基本思想是先将所有边按照权值从小到大排序，然后依次将边加入生成树中，直到生成树中包含了所有的顶点为止。

具体来说，我们可以将所有的顶点看作是一个独立的 *** ，然后逐步合并这些 *** 。在每一次合并的过程中，我们选择一条权值最小的边，将它的两个端点所在的 *** 合并成一个 *** 。这样，当所有的顶点都在同一个 *** 中时，生成的树就是最小生成树。

3. 普里姆算法的原理是什么？

普里姆算法也是一种贪心算法，它的基本思想是从一个任意的顶点开始，不断地向生成树中添加边，直到生成树包含了所有的顶点为止。

具体来说，我们首先将一个任意的顶点加入生成树中，然后将这个顶点所连接的所有边按照权值从小到大排序。然后依次将这些边加入生成树中，如果加入的边所连接的顶点不在生成树中，就将它们加入生成树中。这样，当所有的顶点都在生成树中时，生成的树就是最小生成树。

4. 克鲁斯卡尔算法和普里姆算法的时间复杂度分别是多少？

克鲁斯卡尔算法的时间复杂度是O(ElogE)，其中E表示边的数量。因为我们需要对所有的边进行排序，所以时间复杂度是O(ElogE)。另外，在合并 *** 时，我们需要使用并查集来判断两个顶点是否在同一个 *** 中，这也需要O(ElogE)的时间复杂度。

普里姆算法的时间复杂度是O(ElogV)，其中V表示顶点的数量。因为我们需要对每个顶点的边进行排序，所以时间复杂度是O(ElogV)。另外，在加入边的过程中，我们需要使用优先队列来维护边的顺序，这也需要O(ElogV)的时间复杂度。

5. 克鲁斯卡尔算法和普里姆算法的优缺点分别是什么？

克鲁斯卡尔算法的优点是简单易懂，实现容易。它的缺点是时间复杂度较高，特别是在边的数量很大的时候，效率会非常低。

普里姆算法的优点是时间复杂度较低，特别是在顶点的数量远大于边的数量时，效率会非常高。它的缺点是实现稍微复杂一些，需要使用优先队列来维护边的顺序。

6. 在什么情况下应该选择克鲁斯卡尔算法？在什么情况下应该选择普里姆算法？

如果边的数量很大，而顶点的数量比较小，应该选择克鲁斯卡尔算法。因为在这种情况下，克鲁斯卡尔算法的时间复杂度要比普里姆算法低。

如果顶点的数量很大，而边的数量比较小，应该选择普里姆算法。因为在这种情况下，普里姆算法的时间复杂度要比克鲁斯卡尔算法低。

7. 最小生成树算法还有哪些扩展和应用？

最小生成树算法的扩展和应用还有很多，比如带权图的最短路径问题、 *** 流问题、最小斯坦纳树问题等。在实际应用中，最小生成树算法也被广泛应用于 *** 设计、电路设计、交通规划、城市规划等领域。

总之，最小生成树算法是一种非常重要的算法，在实际应用中有着广泛的应用前景。对于不同的问题和应用场景，我们需要选择不同的最小生成树算法来解决问题。